拓扑物态是凝华态物理学的一个乐不思蜀的前沿范围Ady的电影，展现出一系列卓著传统长入的奇异步地。其中，陈绝缘体看成一类二维系统，因其非平庸的拓扑不变量——陈数而备受怜惜。陈数源于系统的布洛赫波函数的贝里曲率，它决定了系统的拓扑性质，并导致了量子霍尔效应等私有的特征。

传统上，规划陈数频繁袭取周期性界限要求。然则，最近发表在《物理辩驳B》的连络引入了一种新的界限要求——螺旋界限要求，为连络拓扑相提供了私有的视角。螺旋界限要求使东说念主们大致更直不雅、更有用地规划陈数。

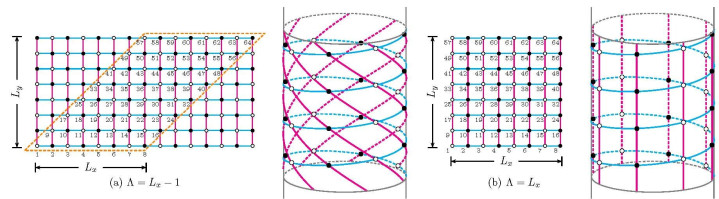
陈数与拓扑相

为了长入陈数，咱们领先需要了解拓扑相的见解。在凝华态物理学中，拓扑相的特征在于其全局性质对系统哈密顿量的平滑变形具有鲁棒性。这些性质由拓扑不变量编码，这些不变量在保抓系统对称性的流畅变换下保抓不变。

在二维系统中，陈数看成一个紧要的拓扑不变量出现。它源于系统的布洛赫波函数的贝里曲率。非零的陈数标明存在一个与平庸能带绝缘体不同的拓扑相。这么的系统施展出权臣的特点，举例量子霍尔效应，其中在磁场存鄙人出现量子化的霍尔电导率。陈数径直决定了这个量子化电导率的值。

螺旋界限要求偏执上风

传统上，陈数是使用周期性界限要求规划的，其中假定系统的波函数在两个空间方进取皆是周期性的。固然这种设施也曾造就，但对于大型系统来说，规划资本可能很高。比较之下，螺旋界限要求提供了一种替代设施，具有以下几个优点：

规划着力：螺旋界限要求允许以一维阵势规划陈数，比较于传统的二维设施，大大裁汰了规划资本。

直不雅判辨注解：螺旋界限要求为系统的拓扑性质提供了更直不雅的图像。通过分析角落态在不同界限要求下的活动，不错径直估计非平庸拓扑相的存在。

无邪性：螺旋界限要求不错诈欺于各样二维系统，包括具有复杂几何结构和无序的系统。

使用螺旋界限要求规划陈数的设施

也曾劝诱了几种使用螺旋界限要求规划陈数的设施。两种主要设施是：

福奎-初塚-铃木（FHS）设施：该设施基于晶格圭表表面，波及向系统中插入一个磁通量。由此产生的垂直标的的有用电流与陈数径直关系。

Coh-Vanderbilt设施：该设施将陈数与系统的电子极化关系起来。通过对系统施加有限的动量扭转，不错从携带的极化电流中索求陈数。

连络标明，螺旋界限要求不错有用用于规划二维系统中的陈数。发现突显了这种设施的各样性，显现其不错处置各样晶格结构和拓扑相。螺旋界限要求的使用不仅简化了规划经过，还提供了对材料拓扑性质的新见地。

影响和诈欺

准确规划陈数的才智对表面连络和骨子诈欺皆有潜入的影响。在表面物理范围，这种设施增强了咱们对拓扑绝缘体、量子霍尔系统和其他奇异相的长入。从诈欺的角度来看，它有助于假想和表征具有私有电子特点的材料，如隆重的界限态和量子化导电性。

论断

美足交

二维系统中具有螺旋界限要求的陈数是一个乐不思蜀且阔气适度的连络范围。螺旋界限要求为长入和表征拓扑相提供了一个有价值的用具Ady的电影，既具有规划着力，又具有直不雅的知致力于。跟着该范围连络的进展，咱们不错期待发现更多对于拓扑材料的令东说念主答应的发现和诈欺。